Pemirsa!! Berikut di bawah ini ditampilkan tugas yang diberikan oleh Bapak Dwi, mengenai program macam - macam distribusi. Monggo disimak gan..
Uniform
Function Uniform (a,b : double) : double;
Var u : double;
Begin
u := random;
Uniform := (b-a) * u + a;
End;
Eksponensial
Function Eksponensial (beta : double) : double;
Var u : double;
Begin
u := random;
Eksponensial := -beta * ln(u);
End;
Normal
Procedure Normal (mean,variance : double ; Var z1,z2 : double);
Var u1,u2,v1,v2,w,y,x1,x2 : double;
Begin
Repeat
u1 := random;
u2 := random;
v1 := 2 * u1 - 1;
v2 := 2 * u2 - 1;
w := sqr(v1) + sqr(v2);
if w <= 1 then
begin
y := sqrt ((-2*ln(w))/w);
x1 := v1 * y;
x2 := v2 * y;
z1 := sqrt (variance) * x1 + mean;
z2 := sqrt (variance) * x2 + mean;
end
Until w <= 1;
End;
Wibull
Function Weibull (alfa,beta: double) : double;
Var u,z : double;
Begin
u := random;
z := -ln(u);
Weibull := beta * exp (ln(z)/alfa);
End;
Lognormal
procedure lognormal (mean,varr : double;
Var zln1,zln2 : double);
Var y1, y2 : double;
begin
Normal (mean,varr,y1,y2);
zln1 := exp(y1);
zln2 := exp(y2);
end;
T-student
function tdistribution(m:integer):double;
{ created :
based on Principles of Random Variate Generation
by John Dagpunar, 1988
published by Claredon Press - OXFORD
please check if any other theory of t-distribution }
Label r2;
Var v,x,r,s,c,a,f,g,mm : real;
begin
mm:=0;
if m < 1 then
begin
writeln('impermissible degrees of freedom.');
halt;
end;
if (m <> mm) then
begin
s:=m;
c:=-0.25*(s+1);
a:=4/power((1+1/s),c);
f:=16/a;
if m>1 then
begin
g:=s-1;
g:=power(((s+1)/g),c)*sqrt((s+s)/g);
end else
g := 1;
mm:=m;
end;
r2:repeat
r:=random;
until r > 0.0;
x:=(2*random-1)*g/r;
v:=x*x;
if (v>(5-a*r)) then
begin
if ((m>=3) and (r*(v+3)>f)) then goto r2;
if (r>power((1+v/s),c)) then goto r2;
end;
tdistribution :=x;
end;
Program Distribusi
Posted by Kadek Agus Satrya Wisesa 0 comments
Labels: Simulation
Bilangan Biner
 Sistem bilangan biner atau sistem bilangan basis dua adalah sebuah sistem penulisan angka dengan menggunakan simbol 0 dan 1. Sistem bilangan modern ini ditemukan oleh Gottfried Wilhelm Leibniz pada abad ke-17. Sistem bilangan ini merupakan dasar dari semua sistem bilangan berbasis digital. Sistem ini bisa disebut juga dengan bit atau binary digit.
Sistem bilangan biner atau sistem bilangan basis dua adalah sebuah sistem penulisan angka dengan menggunakan simbol 0 dan 1. Sistem bilangan modern ini ditemukan oleh Gottfried Wilhelm Leibniz pada abad ke-17. Sistem bilangan ini merupakan dasar dari semua sistem bilangan berbasis digital. Sistem ini bisa disebut juga dengan bit atau binary digit. Misal,
1 = 111 = 3
111 = 7
berapakah 111.......1(32) = ...... ?
Materi Tambahan: Invers Transformasi
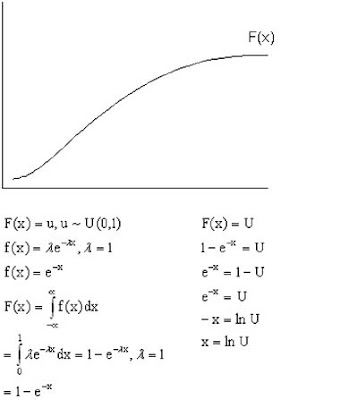
Pendekatan matematis di atas dilakukan untuk mengacak data yang berdistribusi uniform(a,b), commandnya dalam Pascal adalah sebagai berikut!
function uniform(a,b:real) :real;
begin
uniform:=a+(b-a)x random;
end;
Untuk data yang berdistribusi eksponensial:
function expo(mean:real) : real;
begin
uniform:=-log e (random) * mean;
end;
111.......1(32) = (2^k) - 1, dengan k merupakan jumlah bilangan biner '1'. Sehingga bilangan terbesar dalam komputer adalah 32 digit biner. Bila melebihi ini, komputer tidak akan bisa membacanya.
Ingin tahu lebih lanjut mengenai perhitungan sistem bilangan ini dan bilangan lainnya???
Klik di sini!
Ingin tahu lebih lanjut mengenai perhitungan sistem bilangan ini dan bilangan lainnya???
Klik di sini!
Materi Tambahan: Invers Transformasi

Pendekatan matematis di atas dilakukan untuk mengacak data yang berdistribusi uniform(a,b), commandnya dalam Pascal adalah sebagai berikut!
function uniform(a,b:real) :real;
begin
uniform:=a+(b-a)x random;
end;
Untuk data yang berdistribusi eksponensial:
function expo(mean:real) : real;
begin
uniform:=-log e (random) * mean;
end;
{Materi Kuliah Teknik Simulasi, Pak Dwi}
Posted by Kadek Agus Satrya Wisesa 0 comments
Labels: Simulation
Pseudorandom numbers
 Dalam postingan kali ini, kita akan membahas tentang pseudorandom number generation. Apa yang dimaksud dengan Pseudorandom numbers?? Pseudo artinya semu, jadi secara garis besar pseudorandom berarti bilangan acak semu.
Dalam postingan kali ini, kita akan membahas tentang pseudorandom number generation. Apa yang dimaksud dengan Pseudorandom numbers?? Pseudo artinya semu, jadi secara garis besar pseudorandom berarti bilangan acak semu.Salah satu pendekatan untuk membangkitkan pseudorandom numbers dimulai dengan nilai Xo yang bernama seed , dan menghitung secara acak nilai - nilai selanjutnya yaitu Xn, n>=1, dengan rumus,
Xn = AXn-1 Modulo M,
dimana A dan M merupakan bilangan bulat positif, AXn-1 dibagi M dan menghasilkan sisa, yaitu Xn.
Untuk lebih memperjelas, perhatikan contoh perhitungan berikut ini:
Misal,
A = 2Xn = AXn-1 Modulo M,
dimana A dan M merupakan bilangan bulat positif, AXn-1 dibagi M dan menghasilkan sisa, yaitu Xn.
Untuk lebih memperjelas, perhatikan contoh perhitungan berikut ini:
Misal,
M = 5
Xo = 3, maka
X1 = 2(3) Modulo 5 = 1
X2 = 2(1) Modulo 5 = 2
X3 = 2(2) Modulo 5 = 4
X4 = 2(4) Modulo 5 = 3
Kenapa bisa disebut acak semu? Karena hasilnya berulang, yaitu pada saat X4, nilai dari X4 kembali pada Xo, maka disebut acak semu atau pseudorandom. Untuk membuat hasil lebih acak, n perlu dibuat lebih besar. Materi lengkap mengenai Pseudorandom number bisa dilihat di link ini.
{Materi Kuliah Teknik Simulasi, Pak Dwi}
Posted by Kadek Agus Satrya Wisesa 0 comments
Labels: Simulation
Subscribe to:
Posts (Atom)

