Pemirsa!! Berikut di bawah ini ditampilkan tugas yang diberikan oleh Bapak Dwi, mengenai program macam - macam distribusi. Monggo disimak gan..
Uniform
Function Uniform (a,b : double) : double;
Var u : double;
Begin
u := random;
Uniform := (b-a) * u + a;
End;
Eksponensial
Function Eksponensial (beta : double) : double;
Var u : double;
Begin
u := random;
Eksponensial := -beta * ln(u);
End;
Normal
Procedure Normal (mean,variance : double ; Var z1,z2 : double);
Var u1,u2,v1,v2,w,y,x1,x2 : double;
Begin
Repeat
u1 := random;
u2 := random;
v1 := 2 * u1 - 1;
v2 := 2 * u2 - 1;
w := sqr(v1) + sqr(v2);
if w <= 1 then
begin
y := sqrt ((-2*ln(w))/w);
x1 := v1 * y;
x2 := v2 * y;
z1 := sqrt (variance) * x1 + mean;
z2 := sqrt (variance) * x2 + mean;
end
Until w <= 1;
End;
Wibull
Function Weibull (alfa,beta: double) : double;
Var u,z : double;
Begin
u := random;
z := -ln(u);
Weibull := beta * exp (ln(z)/alfa);
End;
Lognormal
procedure lognormal (mean,varr : double;
Var zln1,zln2 : double);
Var y1, y2 : double;
begin
Normal (mean,varr,y1,y2);
zln1 := exp(y1);
zln2 := exp(y2);
end;
T-student
function tdistribution(m:integer):double;
{ created :
based on Principles of Random Variate Generation
by John Dagpunar, 1988
published by Claredon Press - OXFORD
please check if any other theory of t-distribution }
Label r2;
Var v,x,r,s,c,a,f,g,mm : real;
begin
mm:=0;
if m < 1 then
begin
writeln('impermissible degrees of freedom.');
halt;
end;
if (m <> mm) then
begin
s:=m;
c:=-0.25*(s+1);
a:=4/power((1+1/s),c);
f:=16/a;
if m>1 then
begin
g:=s-1;
g:=power(((s+1)/g),c)*sqrt((s+s)/g);
end else
g := 1;
mm:=m;
end;
r2:repeat
r:=random;
until r > 0.0;
x:=(2*random-1)*g/r;
v:=x*x;
if (v>(5-a*r)) then
begin
if ((m>=3) and (r*(v+3)>f)) then goto r2;
if (r>power((1+v/s),c)) then goto r2;
end;
tdistribution :=x;
end;
Program Distribusi
Posted by Kadek Agus Satrya Wisesa 0 comments
Labels: Simulation
Bilangan Biner
 Sistem bilangan biner atau sistem bilangan basis dua adalah sebuah sistem penulisan angka dengan menggunakan simbol 0 dan 1. Sistem bilangan modern ini ditemukan oleh Gottfried Wilhelm Leibniz pada abad ke-17. Sistem bilangan ini merupakan dasar dari semua sistem bilangan berbasis digital. Sistem ini bisa disebut juga dengan bit atau binary digit.
Sistem bilangan biner atau sistem bilangan basis dua adalah sebuah sistem penulisan angka dengan menggunakan simbol 0 dan 1. Sistem bilangan modern ini ditemukan oleh Gottfried Wilhelm Leibniz pada abad ke-17. Sistem bilangan ini merupakan dasar dari semua sistem bilangan berbasis digital. Sistem ini bisa disebut juga dengan bit atau binary digit. Misal,
1 = 111 = 3
111 = 7
berapakah 111.......1(32) = ...... ?
Materi Tambahan: Invers Transformasi
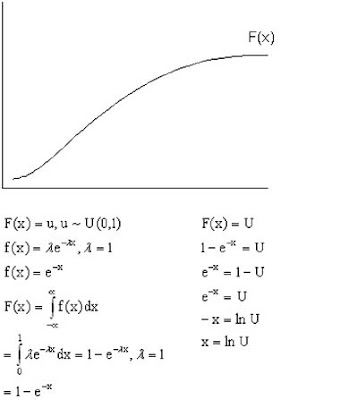
Pendekatan matematis di atas dilakukan untuk mengacak data yang berdistribusi uniform(a,b), commandnya dalam Pascal adalah sebagai berikut!
function uniform(a,b:real) :real;
begin
uniform:=a+(b-a)x random;
end;
Untuk data yang berdistribusi eksponensial:
function expo(mean:real) : real;
begin
uniform:=-log e (random) * mean;
end;
111.......1(32) = (2^k) - 1, dengan k merupakan jumlah bilangan biner '1'. Sehingga bilangan terbesar dalam komputer adalah 32 digit biner. Bila melebihi ini, komputer tidak akan bisa membacanya.
Ingin tahu lebih lanjut mengenai perhitungan sistem bilangan ini dan bilangan lainnya???
Klik di sini!
Ingin tahu lebih lanjut mengenai perhitungan sistem bilangan ini dan bilangan lainnya???
Klik di sini!
Materi Tambahan: Invers Transformasi

Pendekatan matematis di atas dilakukan untuk mengacak data yang berdistribusi uniform(a,b), commandnya dalam Pascal adalah sebagai berikut!
function uniform(a,b:real) :real;
begin
uniform:=a+(b-a)x random;
end;
Untuk data yang berdistribusi eksponensial:
function expo(mean:real) : real;
begin
uniform:=-log e (random) * mean;
end;
{Materi Kuliah Teknik Simulasi, Pak Dwi}
Posted by Kadek Agus Satrya Wisesa 0 comments
Labels: Simulation
Pseudorandom numbers
 Dalam postingan kali ini, kita akan membahas tentang pseudorandom number generation. Apa yang dimaksud dengan Pseudorandom numbers?? Pseudo artinya semu, jadi secara garis besar pseudorandom berarti bilangan acak semu.
Dalam postingan kali ini, kita akan membahas tentang pseudorandom number generation. Apa yang dimaksud dengan Pseudorandom numbers?? Pseudo artinya semu, jadi secara garis besar pseudorandom berarti bilangan acak semu.Salah satu pendekatan untuk membangkitkan pseudorandom numbers dimulai dengan nilai Xo yang bernama seed , dan menghitung secara acak nilai - nilai selanjutnya yaitu Xn, n>=1, dengan rumus,
Xn = AXn-1 Modulo M,
dimana A dan M merupakan bilangan bulat positif, AXn-1 dibagi M dan menghasilkan sisa, yaitu Xn.
Untuk lebih memperjelas, perhatikan contoh perhitungan berikut ini:
Misal,
A = 2Xn = AXn-1 Modulo M,
dimana A dan M merupakan bilangan bulat positif, AXn-1 dibagi M dan menghasilkan sisa, yaitu Xn.
Untuk lebih memperjelas, perhatikan contoh perhitungan berikut ini:
Misal,
M = 5
Xo = 3, maka
X1 = 2(3) Modulo 5 = 1
X2 = 2(1) Modulo 5 = 2
X3 = 2(2) Modulo 5 = 4
X4 = 2(4) Modulo 5 = 3
Kenapa bisa disebut acak semu? Karena hasilnya berulang, yaitu pada saat X4, nilai dari X4 kembali pada Xo, maka disebut acak semu atau pseudorandom. Untuk membuat hasil lebih acak, n perlu dibuat lebih besar. Materi lengkap mengenai Pseudorandom number bisa dilihat di link ini.
{Materi Kuliah Teknik Simulasi, Pak Dwi}
Posted by Kadek Agus Satrya Wisesa 0 comments
Labels: Simulation
Estimator
 Bagaimanakah seorang statistikawan bekerja? Apakah setiap karakteristik dari populasi dipelajari? Ternyata tidak, statistikawan tidak bekerja langsung pada populasi, diperlukan waktu, tenaga, dan perhatian yang lebih untuk mendefinisikan populasi secara detil. Oleh karena sangat rumit untuk mempelajari populasi secara menyeluruh, maka hanya sebagian kecil dari populasi yang dipelajari, yaitu yang disebut dengan sampel, sampel diambil dari populasi dan digunakkan untuk mengestimasi karakteristik dari populasi itu sendiri. Apa saja kriteria estimator yang baik? Diantaranya adalah unbiassed.
Bagaimanakah seorang statistikawan bekerja? Apakah setiap karakteristik dari populasi dipelajari? Ternyata tidak, statistikawan tidak bekerja langsung pada populasi, diperlukan waktu, tenaga, dan perhatian yang lebih untuk mendefinisikan populasi secara detil. Oleh karena sangat rumit untuk mempelajari populasi secara menyeluruh, maka hanya sebagian kecil dari populasi yang dipelajari, yaitu yang disebut dengan sampel, sampel diambil dari populasi dan digunakkan untuk mengestimasi karakteristik dari populasi itu sendiri. Apa saja kriteria estimator yang baik? Diantaranya adalah unbiassed.1 . Estimator tak bias ( mean )
 , apabila terdapat sekumpulan data sebagai berikut,
, apabila terdapat sekumpulan data sebagai berikut,Contoh 1:

maka perhitungan sistematisnya adalah sebagai berikut,

karena nilai ekspektasi tersebut sama dengan nilai parameter, maka estimator tersebut dikatakan tidak bias.
2. Estimator tak bias ( varians )
Dalam statistika deskriptif, variasi merupakan ukuran keragaman untuk mengukur variabilitas dari kumpulan data. Variasi dapat dibedakan menjadi 2 yaitu:
- 1. Variasi untuk populasi
- 2. Variasi untuk sampel
Kedua rumus di atas akan dibandingkan dengan menggunakan contoh simulasi melalui software Minitab. Berikut diberikan algoritmanya:
- 1. Bangkitkan data yang berdistribusi normal dengan mean 60 dan varians 1 sebanyak 100 sebagai populasi
- 2. Ambil 10 sampel (n=10) sebanyak 10 (m=10)
- 3. Hitung varians tiap sampel dan populasi
- 4. Bandingkan varians dari sampel dan populasi. Bila varians sampel sama dengan varians populasi maka estimator dikatakan tidak bias, sebaliknya bila varians sampel tidak sama dengan varians populasi maka estimator dikatakan tidak bias.
Posted by Kadek Agus Satrya Wisesa 0 comments
Labels: Simulation
UPDATE!!!
Kepada AssDos:
Mas Senja n Mbak Lutfi...
Kl mau nge-check update-an baru dari blog ini, pilih ja post update ini ok! disini tiap update-an akan diberitahukan beserta tanggal updatenya, suwun.....
Update 1 (6-9-09):
- 1. Postingan baru: Manfaat Simulasi, Menaksir phi,
- 2. Tambahan materi dalam posting: Contoh penerapan simulasi,
- 1. Postingan baru: Estimator,
- 2. Tambahan materi dalam posting: -
- 1. Postingan baru: Pseudonumbers, Bilangan biner, Program Distribusi
- 2. Tambahan materi dalam posting: -
Posted by Kadek Agus Satrya Wisesa 0 comments
Labels: UPDATE
Menaksir Phi
 Apa itu phi? 3.14? 22/7? Apakah phi merupakan bilangan rasional (bilangan yang bisa ditulis sebagai pecahan) ? Menurut Bapak Dwi, dosen mata kuliah teknik simulasi Institut Teknologi Sepuluh Nopember, phi bukanlah 3.14 ataupun 22/7, phi juga bukan merupakan bilangan rasional. lalu apa yang dimaksud dengan phi?
Apa itu phi? 3.14? 22/7? Apakah phi merupakan bilangan rasional (bilangan yang bisa ditulis sebagai pecahan) ? Menurut Bapak Dwi, dosen mata kuliah teknik simulasi Institut Teknologi Sepuluh Nopember, phi bukanlah 3.14 ataupun 22/7, phi juga bukan merupakan bilangan rasional. lalu apa yang dimaksud dengan phi?Berikut akan diberikan sebuah program yang bisa menaksir harga phi, tetapi sebelumnya perhatikan gambar lingkaran dalam persegi disamping ini. Apabila kita anggap gambar tersebut sebuah target shooting range, maka terdapat tiga kemungkinan tempat jatuhnya peluru, yaitu:
- A. Dalam lingkaran,
- B. Di luar lingkaran tetapi di dalam persegi,
- C. Di luar persegi.
Pendekatan secara sistematis dilakukan terhadap penelitian ini, dimana rasio perbandingan luas lingkaran terhadap luas persegi berbanding lurus dengan jumlah peluru yang jatuh di dalam lingkaran terhadap jumlah peluru yang jatuh di dalam persegi. Hasil akhir dari perhitungan ini akan menghasilkan sebuah taksiran phi. Perhitungan lengkap bisa anda simak dalam gambar berikut ini!

Sebelum dilanjutkan ke bagian pemrograman, terlebih dahulu perlu diketahui apa saja syarat sebuah peluru jatuh di dalam maupun di luar lingkaran, perhatikan gambar di bawah ini!
Dalam gambar di atas, terdapat sebuah seperempat lingkaran dengan jari - jari 1, maka persamaan lingkarannya adalah x^2 + y^2 = 1, x dan y berdistribusi uniform. Sebuah peluru dikatakan jatuh di dalam lingkaran bila x^2 + y^2 < 1, dan sebaliknya jatuh di luar lingkaran bila x^2 + y^2 > 1.
Program penaksir phi ini dibuat dengan bantuan software pascal. Bagaimana konsep program penaksir ini bekerja? Seperti yang dijelaskan di atas, program ini bekerja dengan cara menghitung rasio jumlah peluru yang jatuh yang jatuh di dalam ataupun di luar lingkaran. Algoritma program ini akan dipaparkan dalam langkah - langkah berikut:
- 1. Terlebih dahulu deklarasikan variabel - variabel yang digunakan
- 2. Misalkan banyaknya percobaan m = 1000, dan untuk masing - masing percobaan akan diambil sampel sebanyak n = 10000, artinya untuk 1x percobaan peluru sebanyak 10000 akan ditembakkan ke dalam target. Pengambilan titik peluru sebanyak 10000 ini bersifat random, jadi tidak mungkin terjadi pengulangan.
- 3. Bila kita melakukan 1000 percobaan, maka akan dihasilkan phi sebanyak 1000, misal s merupakan jumlah dari phi secara keseluruhan.
- 4. Setelah mendapatkan jumlah dari keseluruhan phi, perlu diketahui rata - rata phi yang bermunculan, jadi bagilah s dengan jumlah percobaan, yaitu 1000.
- 5. Misalkan variabel p merupakan hasil rata - rata dari phi, variabel inilah yang merupakan taksiran phi.

setelah di-run, akan menghasilkan output (taksiran phi) sebagai berikut!
Posted by Kadek Agus Satrya Wisesa 0 comments
Labels: Simulation
Manfaat Simulasi
 Simulasi digunakan sebelum sebuah sistem yang ada dibangun dengan manfaat:
Simulasi digunakan sebelum sebuah sistem yang ada dibangun dengan manfaat:
- 1. To reduce the chance of failure to meet specifications,
- 2. To eliminate unforeseen bottlenecks,
- 3. To prevent under or over utilization of resource,
- 4. To optimize system performance.
{Modul Teknk Simulasi - Prof Drs Nur Irawan MIKom PhD }
Posted by Kadek Agus Satrya Wisesa 0 comments
Labels: Simulation
Subscribe to:
Comments (Atom)